实验设计期中复习
参数估计
期望和方差
期望计算公式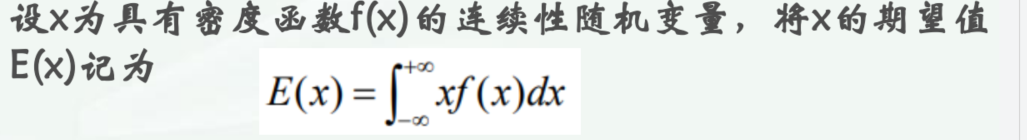
方差计算公式 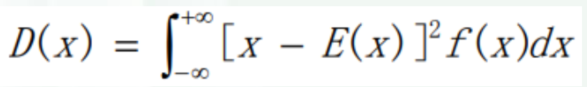
点估计
初衷:由于无法用无穷的点来算(积分),因此采用有限的点来进行估计
使用最大似然法,构造极大似然函数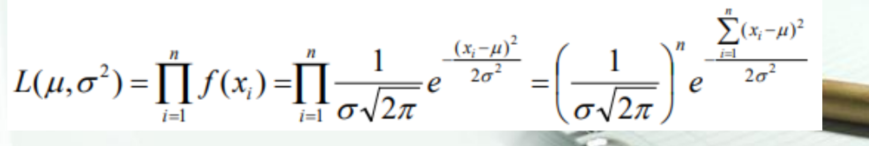
通过解方程,使得解满足极大似然函数值达到最大,有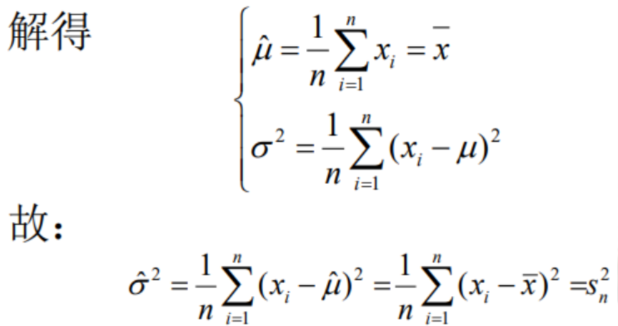
该结果是极大似然函数的点估计
- 无偏性,点估计的期望与n无关,因此对点估计的方差进行校正
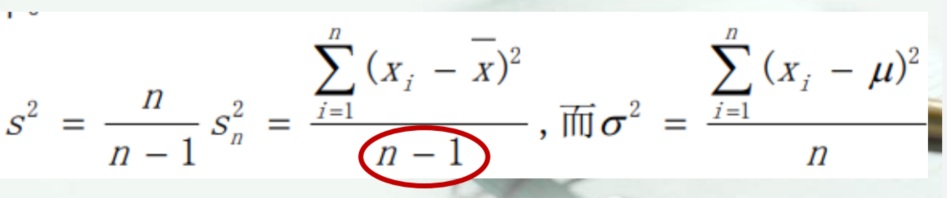
- 有效性:方差小的估计量有效
区间估计
$\hat{X}$作为μ的估计值,同时具有无偏性、有效性和充分性, 但是随机变量 不可能恰好落在μ上,点估计有不足之处。 但是可以用一个区间去包含μ
- 已知多个点对均值的区间估计
公式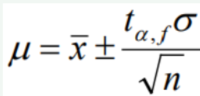
t根据$\alpha,f$查表,$\sigma$标准差,平均平方和开根号,$n$样本量
例题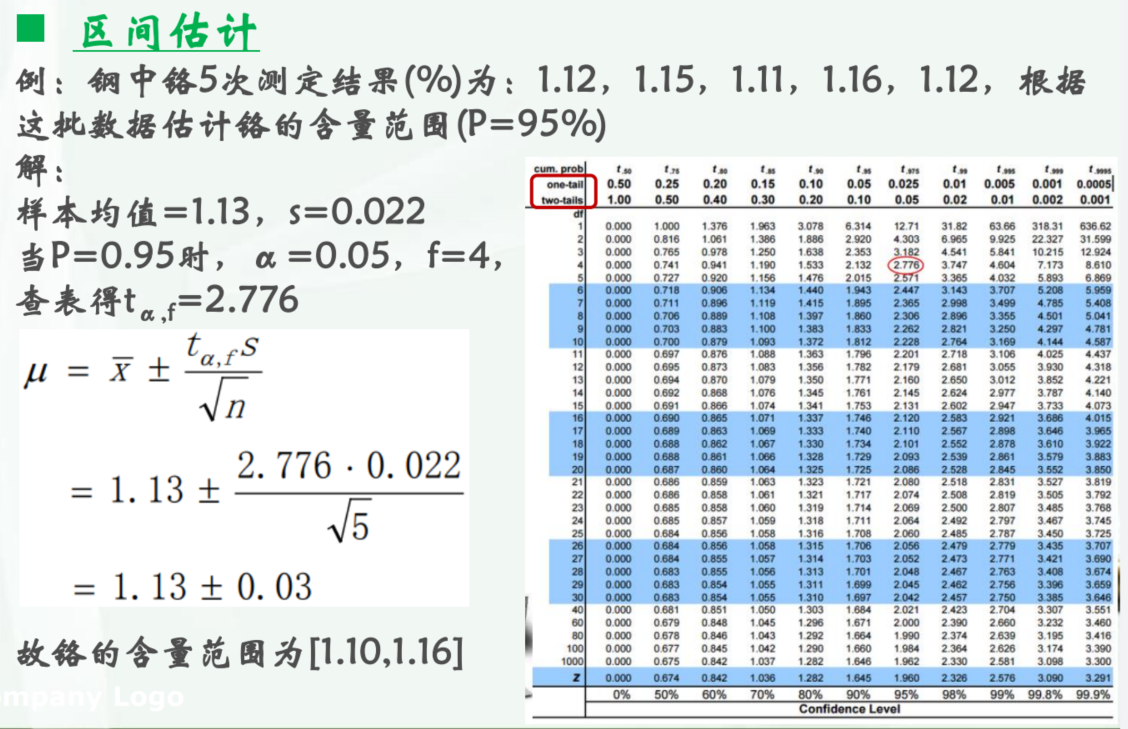
样本容量确定(均值估计样本量)
解决的问题:多少样本才是对分析最佳的?
- 样本量过大,虽然可以提高统计推断精度,但是成 本随之增加;
- 样本量过小,会使统计推断误差过大;
公式推导: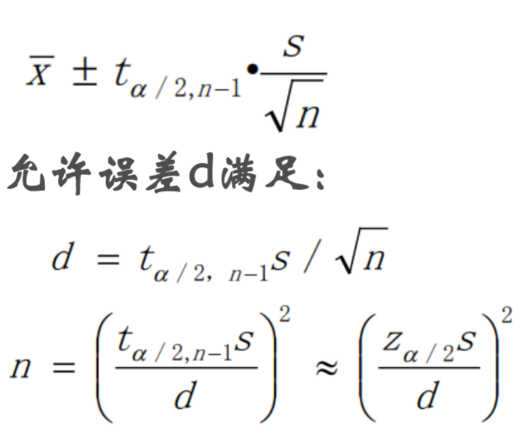
例题 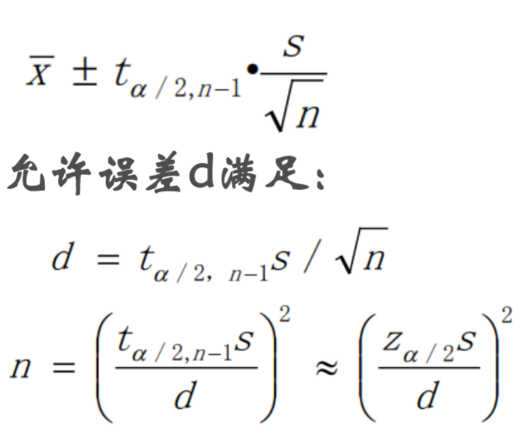
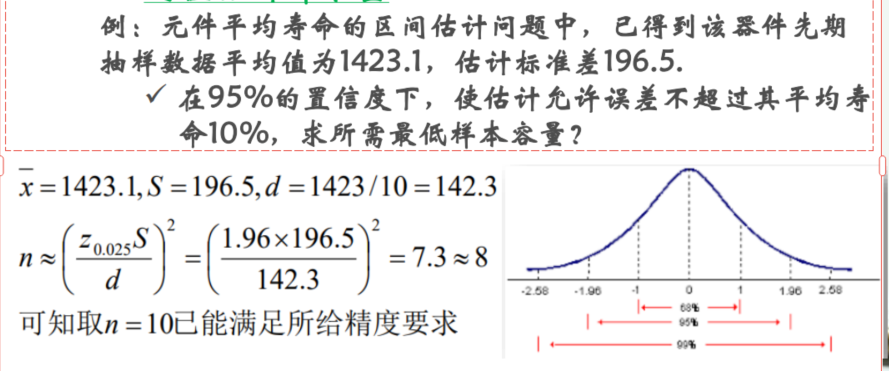
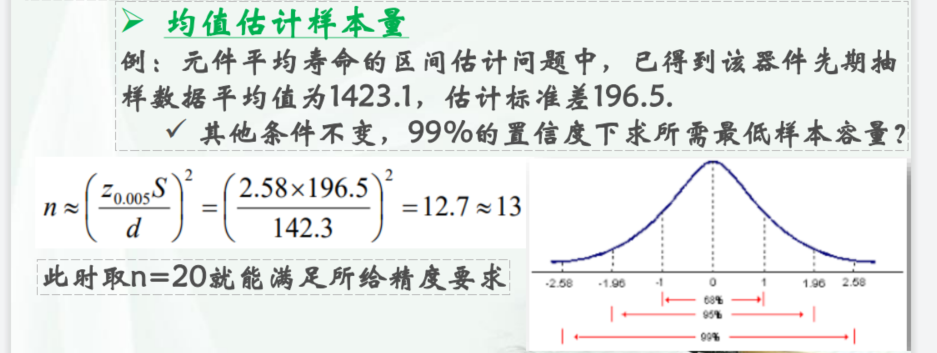
表: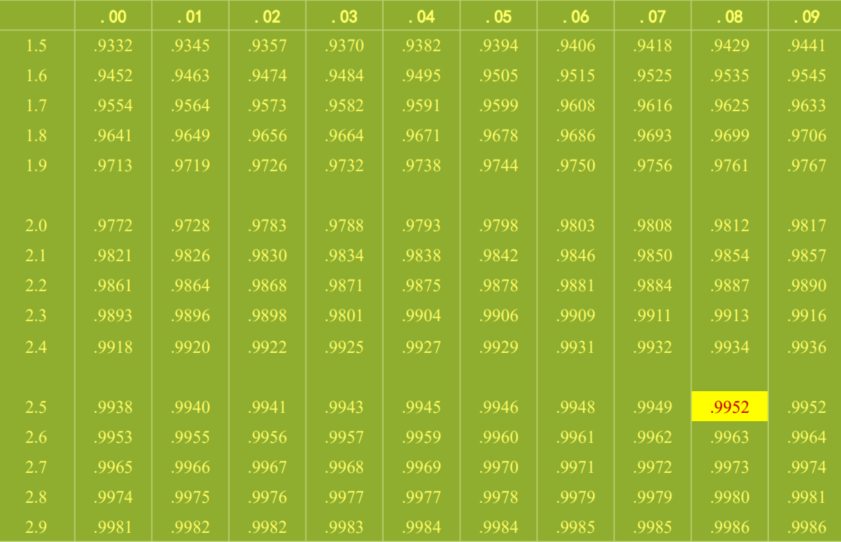
例题解析:
例题1
根据公式,均值方差给定,d=均值x允许误差(10%),$\alpha=0.95,\alpha/2=0.975$
这个实际原理是:
当我们谈论95%的置信区间时,我们通常是在讨论中心的95%,这将留下2.5%在每侧的尾部。因此,为了找到与上侧2.5%相对应的Z分数,我们需要找到表中累积到0.9750(因为 0.5 + 0.475 = 0.975)的值,这意味着中心到Z分数点的面积占总面积的97.5%。
找点:
找表格中累计达到0.975的点,找到横坐标1.9,纵坐标.06,因此z为1.96例题2
同理,得出$\alpha=0.99,\alpha/2=0.995$,读表找出对应的横坐标2.5,纵坐标.08,因此z为2.58
样本总量确定(总体比例估计样本量)
已知次品率,求总体n,未知次品率的情况下,p=0.5保证结果可靠性(图例题二)
例题1
解析 :
- 代入次品率p,d为误差控制,置信度查表0.025表示表格中到达0.975的值
例题2
解析:
- 为保证结果可靠性,取p=0.5,同理计算即可
统计检验
原理
- 此矛盾是从实际推断和原理的矛盾,即“小概率事件在 一次实验中几乎不可能发生”
- 若在一次实验中发生了小概率事件,则拒绝原假设,否 则接受假设
步骤:
数据分布检验
偏度峰度检验
若总体为正态分布,随机抽取样本研究, 偏度g1和峰度g2都服从正态分布
计算公式 :
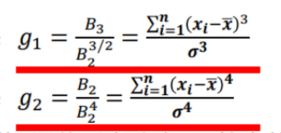
例题: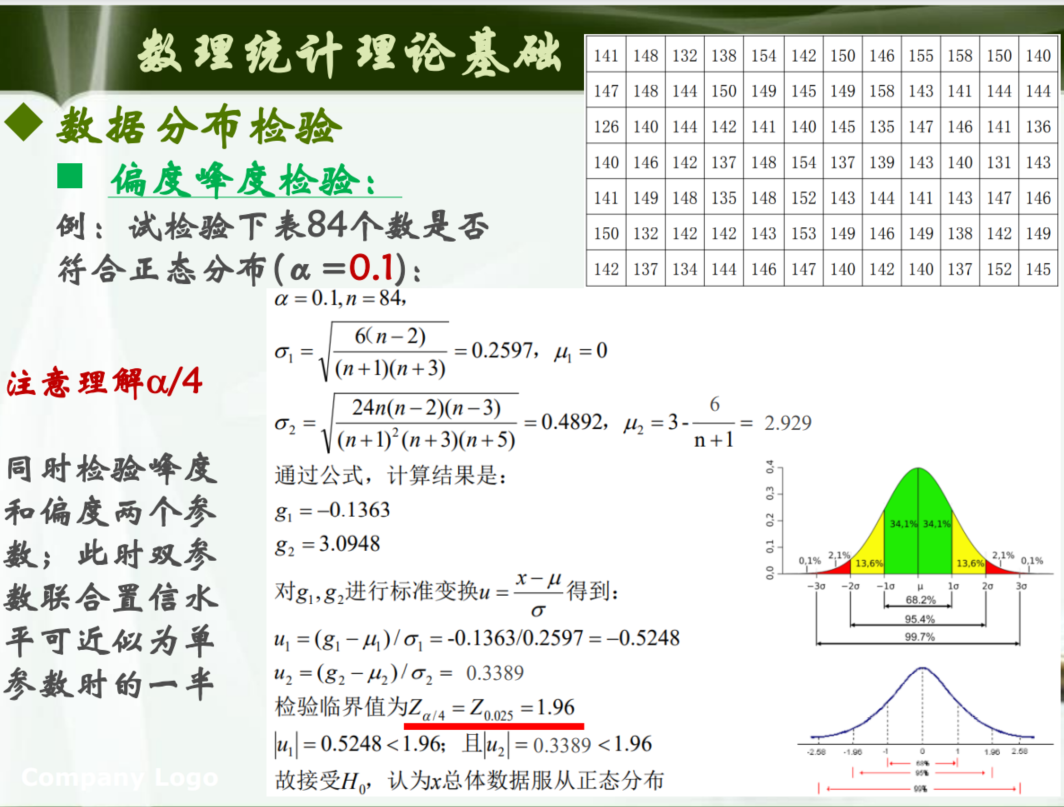
注意$\alpha/4$,多个检验统计量的时候就要多除一个
例题解析 :
按照计算公式,先计算出$g_1$和$g_2$,然后代入$u_i=u(g_i,n)$进行计算,通过比较检验临界值得出结论
K-S分布检验
用于检验检验一组样本数据 的实际分布是否与某一指定的理论分布相符合。简单来说就是能否用正态分布函数来拟合这组样本量,通过构造假设统计量检查最大的误差,来进行假设验证
例题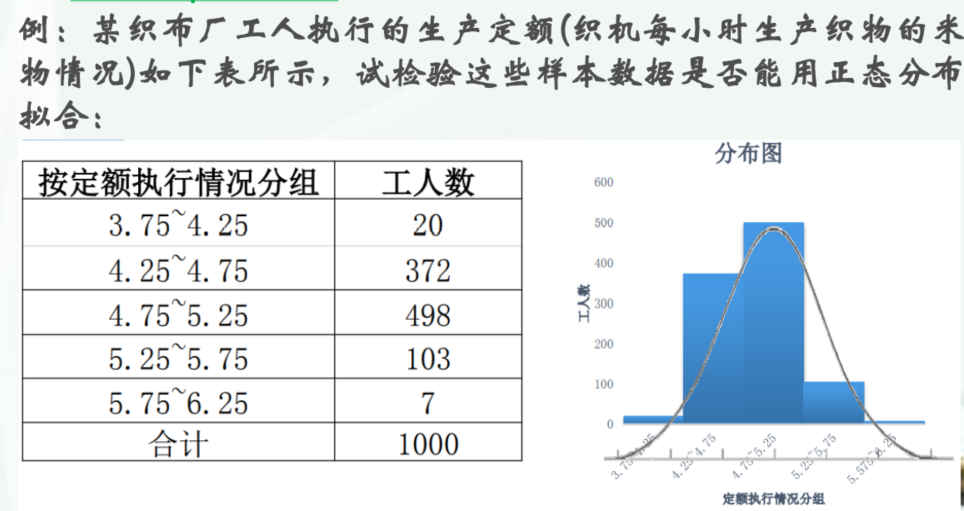
例题解析 :
- 计算样本均值和方差
u = 4.8525 # 计算方差 s = ((4-4.8525)**2 *20 +(4.5-4.8525)**2 *372 +(5-4.8525)**2*498+(5.5-4.8525)**2 * 103+(6-4.8525)**2*7)/999** 0.5 0.3521274627176926 - 作为正态分布u和s的假设,
- H0:样本服从均值=4.85,标准差=0.352的正态分布 •
- H1:样本不服从均值=4.85,标准差=0.352的正态分布
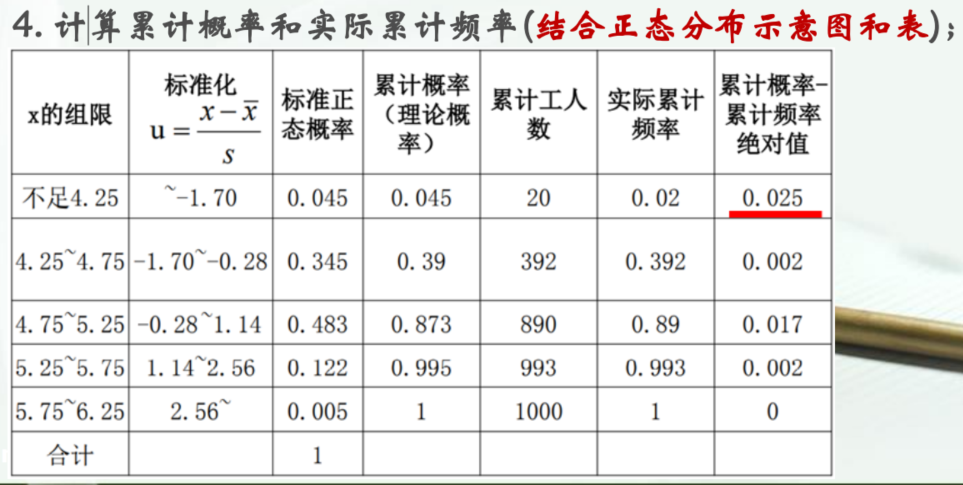
每一列解析(第二行为例)代入4.25和4.75,得出在对应的标准化正态分布中的实际分布区间;查表得该区间的概率($X_{-0.28}-X_{-1.70}$,注由于对称性,表中只有正值,相应变换一下即可,另外表中给的也是累计概率分布$F(x)$),得出累计概率(与前面的累加),实际的累计工人以及累计频率,相减
得出最大概率-频率区间(这个就是$D_n$)
最后计算实际的临界值(根据n和$\alpha$查表即可),然后看看接受还是拒绝解设
卡方拟合优度检验 (可能考)
检验抽取样本的总体分布与某种 特定分布的符合程度
具体步骤
卡方计算公式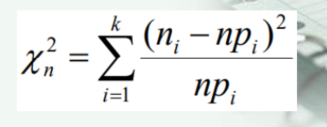
例题: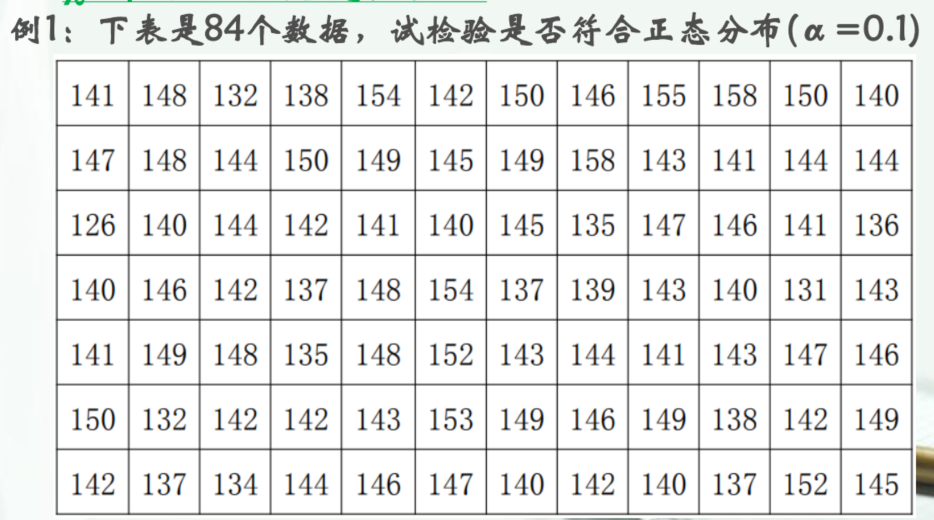
解析:
- 区间划分
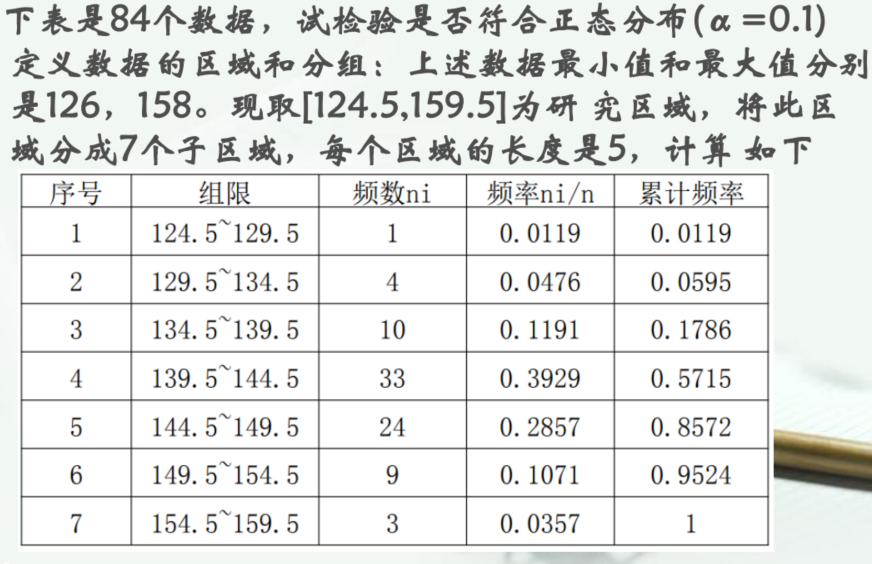
- 计算相应的理论分布
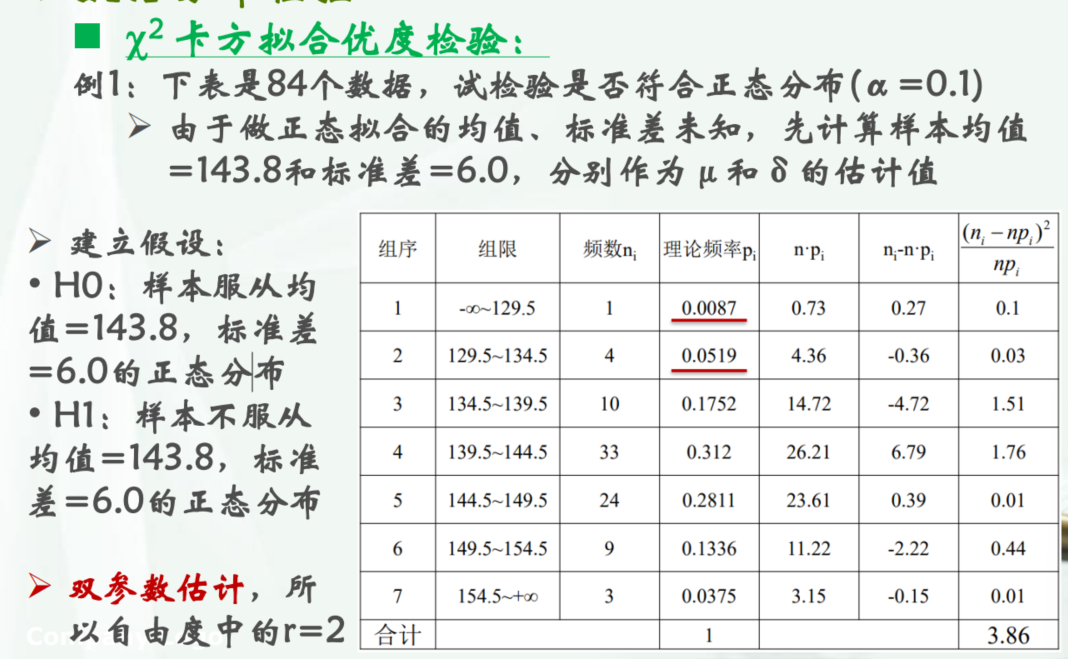
先计算均值和标准差。然后与上一节[[#K-S分布检验]]相同,计算正态分布下的对应理论频率分布,以第一行为例,可以算得(129.5-143.8)/6=-2.3833333,查表得
因此为0.0087。后面代入公式计算得到卡方和即可。检验 量计算方式为: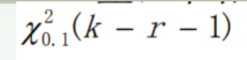
其中0.1为置信水平,k=划分的区间数,r为参数估计数量(正态分布为2),查表
例题2
用上面的方法也能做[[#假设检验]],但是理论上这种方法好一点。
本质上就是划分为良品和不合格品两个区间,然后相应的计算就行。
列联表
表示形式为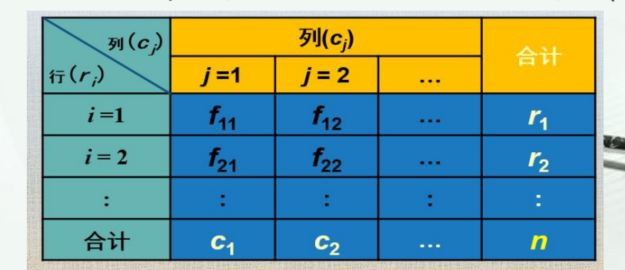
记住计算公式
边界值为X((r-1)(c-1))
例题 :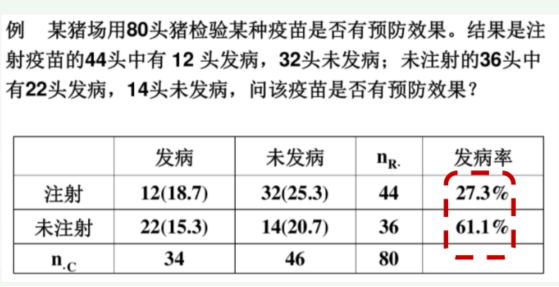
直接代入公式计算就行:
离群值检验
相关应用——异常数据的取舍
四种方法
拉依达准则(3σ准则)

简单算一下就行了
肖维特(Chauvent)准则
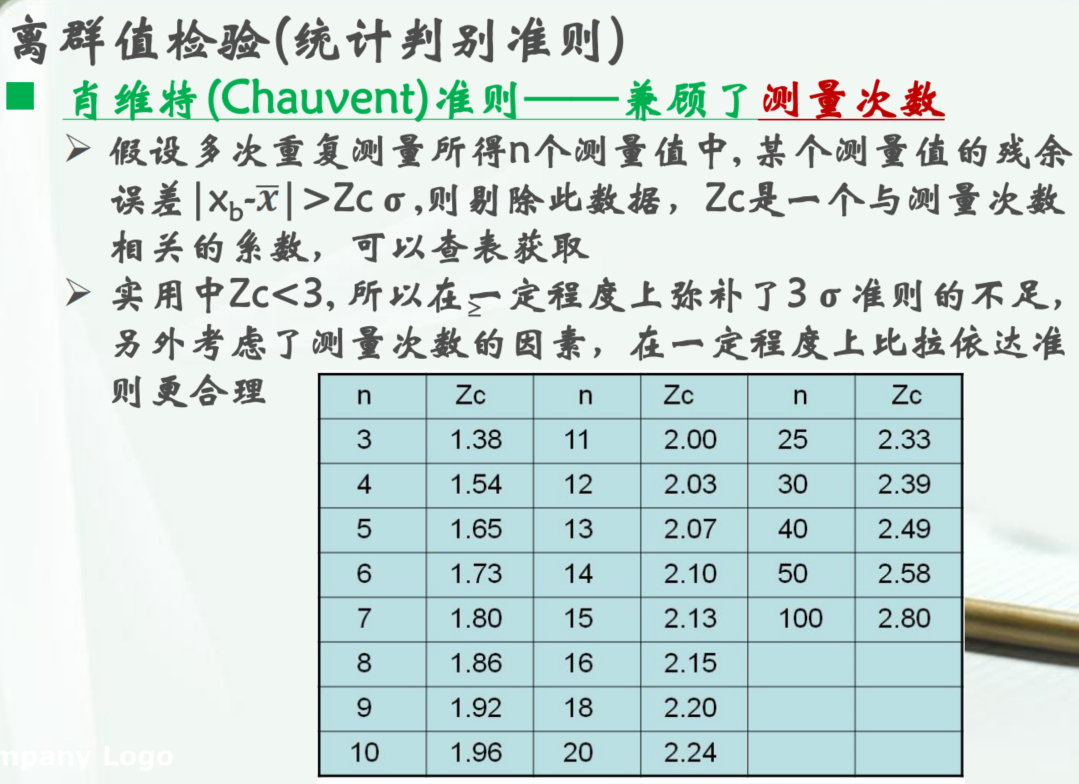
格拉布斯(Grubbs)准则——兼顾了置信概率(可能考)
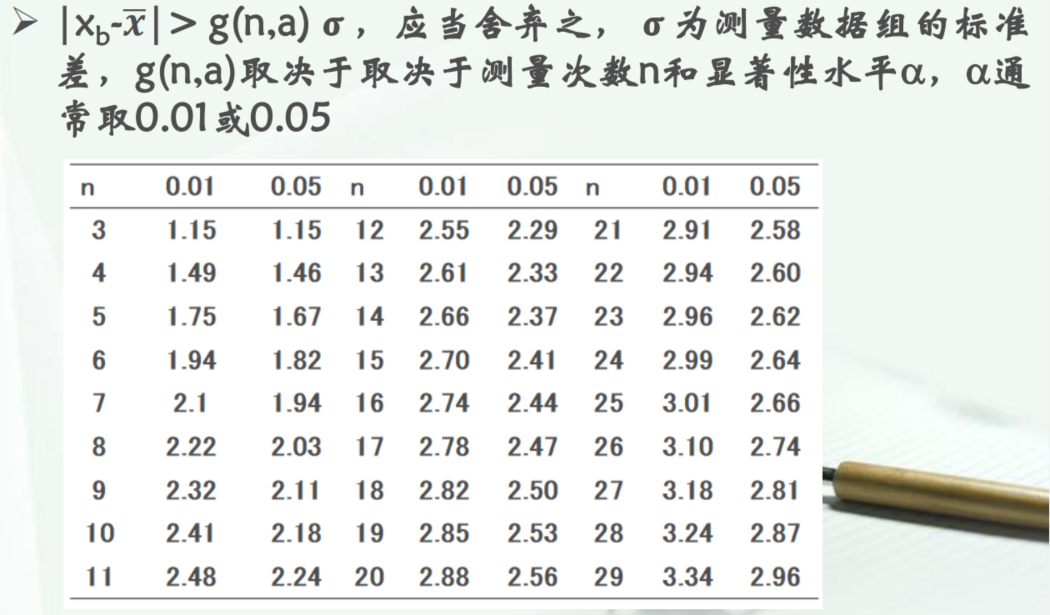
比上面那个多了个置信概率
例题
主要是方差计算公式,这个是样本方差要n-1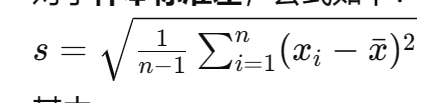
其他的都是按步骤来就行
剔除之后再算一遍
狄克逊准则——通过极差比判定剔除异常数据
异常数据应该是最大数据和最小数据,因此 其基本方法是将数据按大小排队,检验最大数据和最小 数据是否异常数据
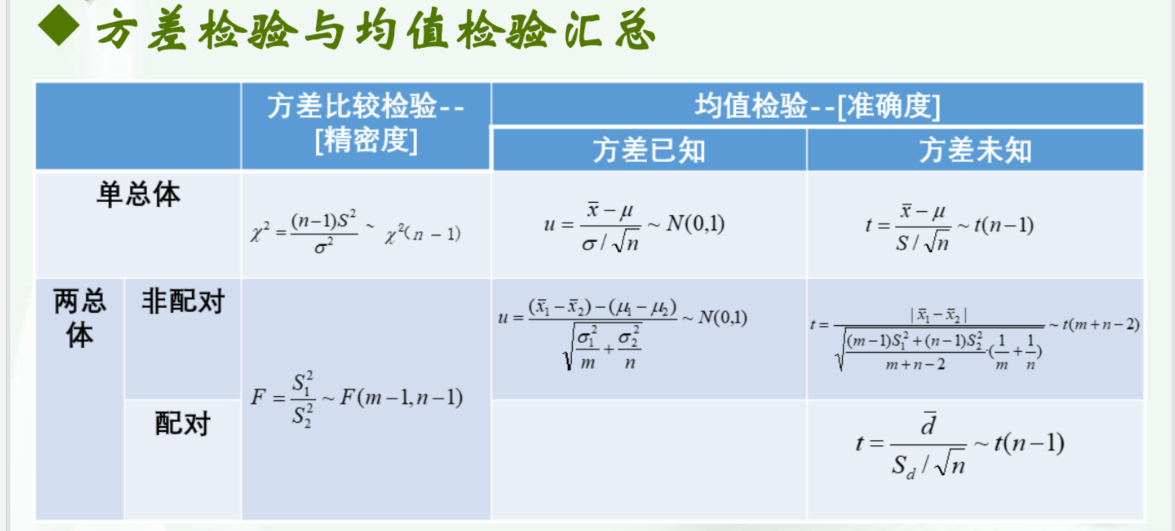
方差比较检验
需要区别单方差检验与多方差检验
其中S为样本标准差,$\sigma$为总体标准差
单方差检验例题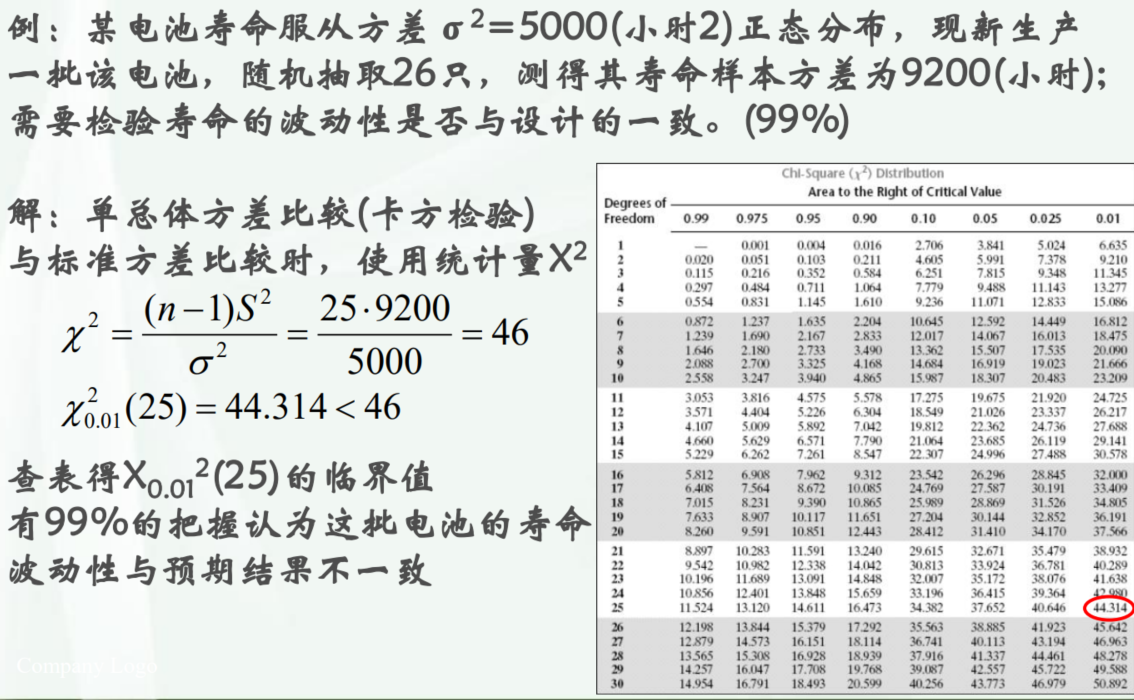
代入数据就行 ,注意卡方是n-1
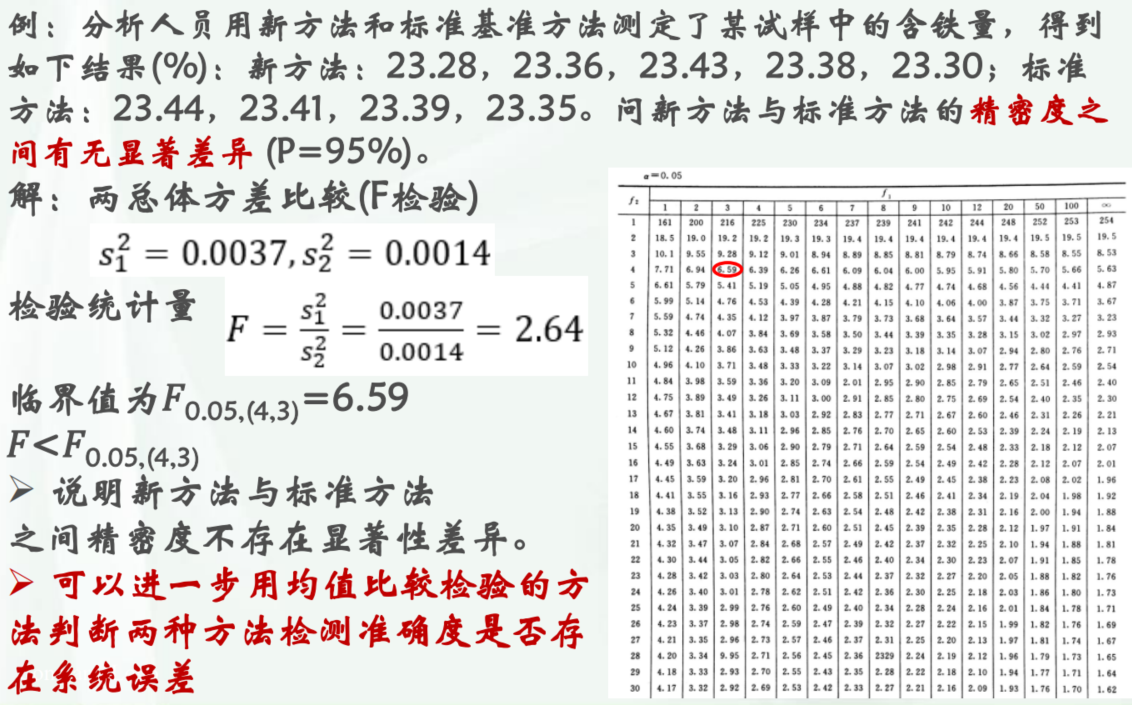
注意是F(m-1,n-1)
(0.07**2+0.01**2+0.08**2+0.03**2+0.05**2)/4=0.0037计算F以及临界值比较
均值检验
分
μ检验(方差已知)
计算公式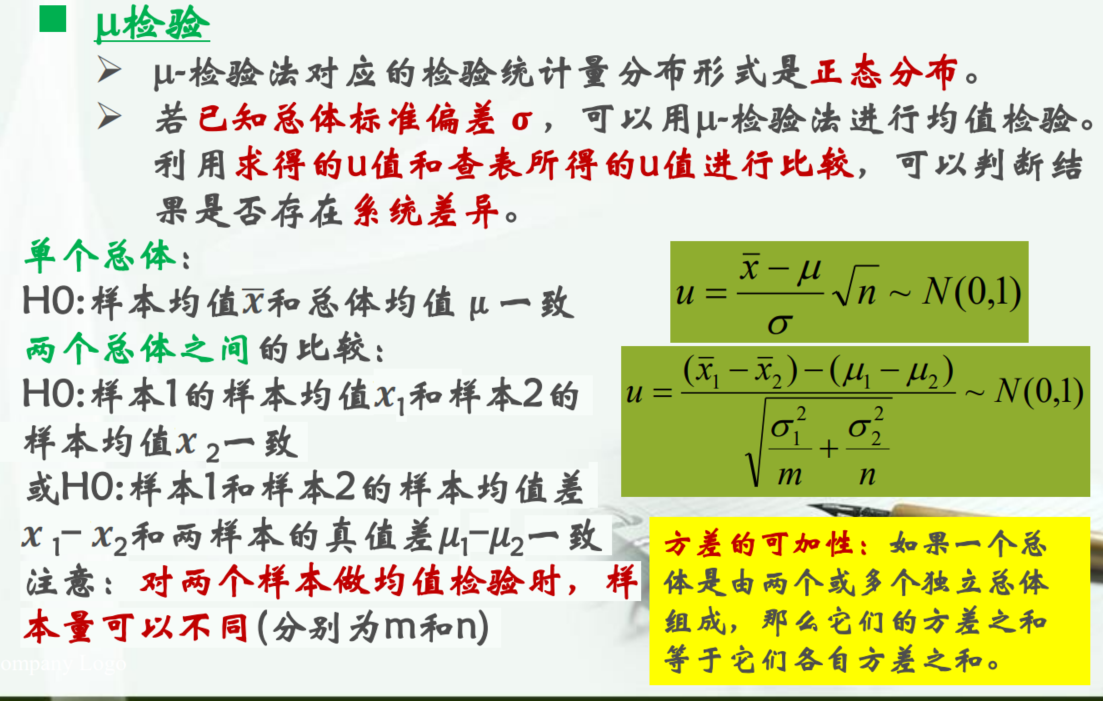
例题
其中μ就是正态分布的分布表的值
t检验(方差未知)
单分布计算公式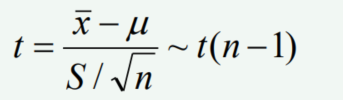
s是样本标准差

双分布计算公式

例题
解析:配对的情况

非配对情况
方差分析
方差分析概述
单因素方差分析
计算公式
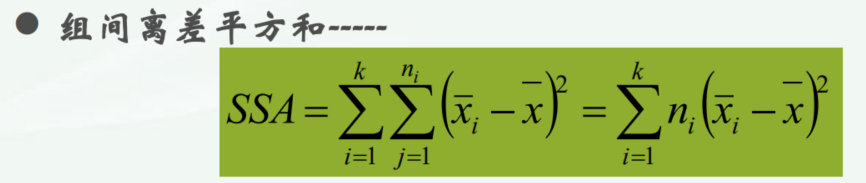


例题: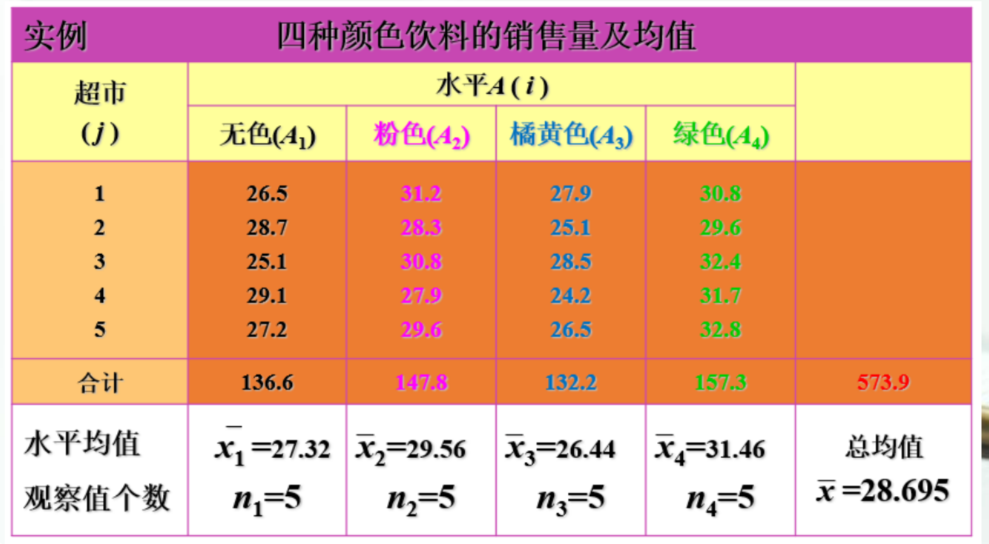
计算: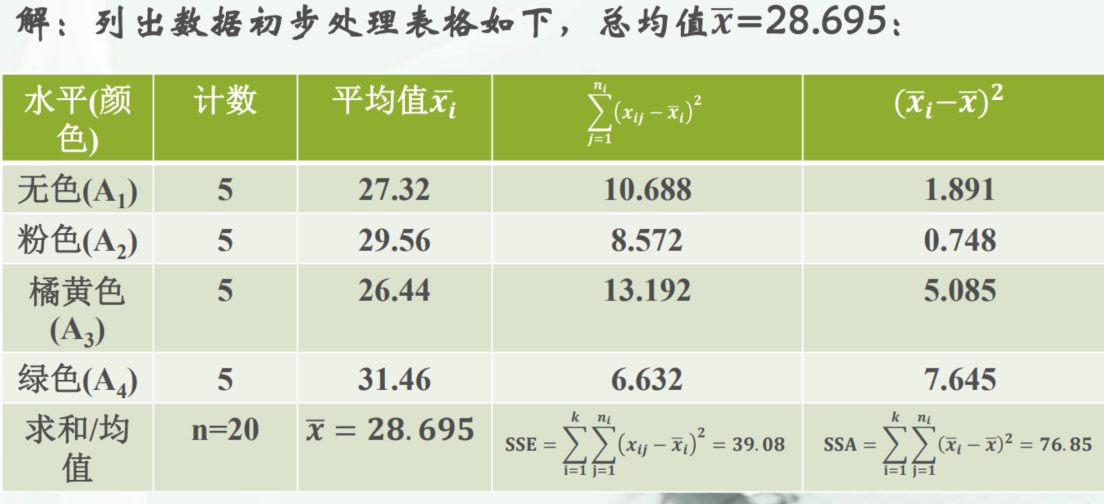
解析:根据公式来就行,SSE组内的方差的和,SSA组间(和总体的均值)的和


例题2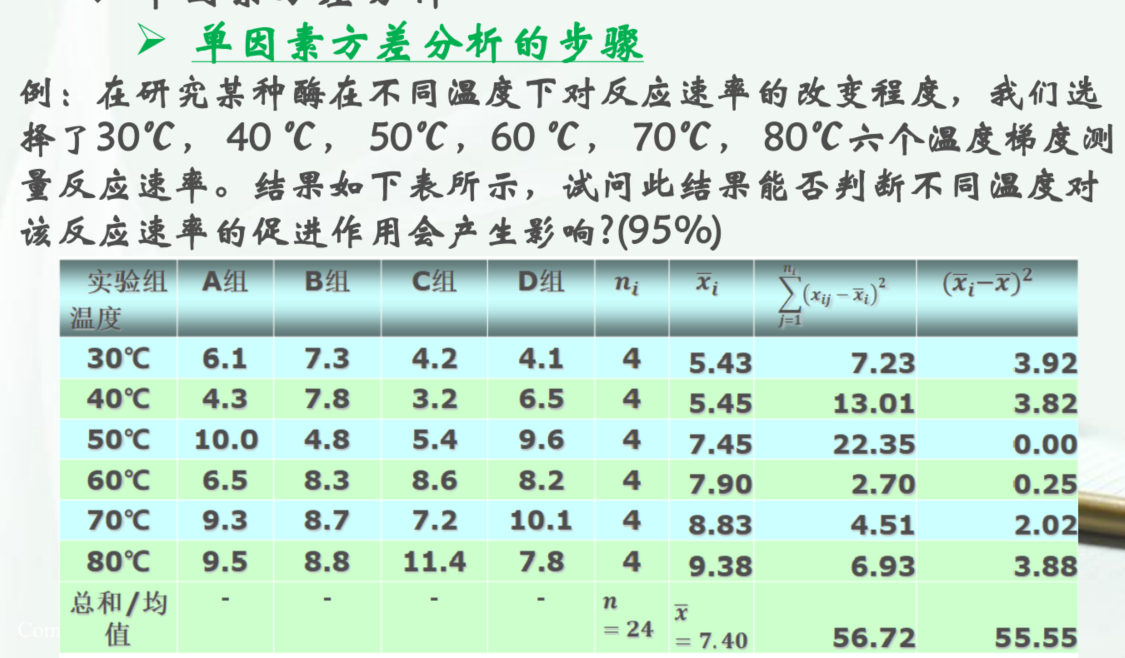
计算SSA和SSE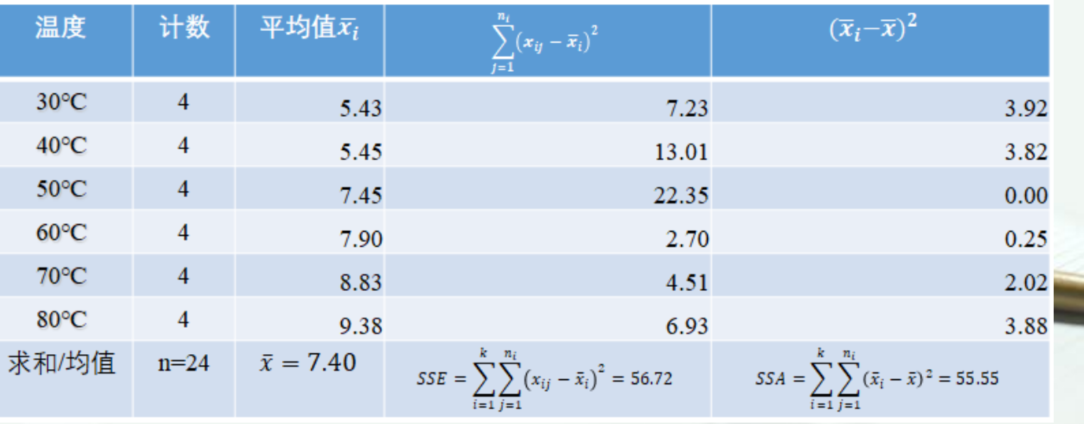
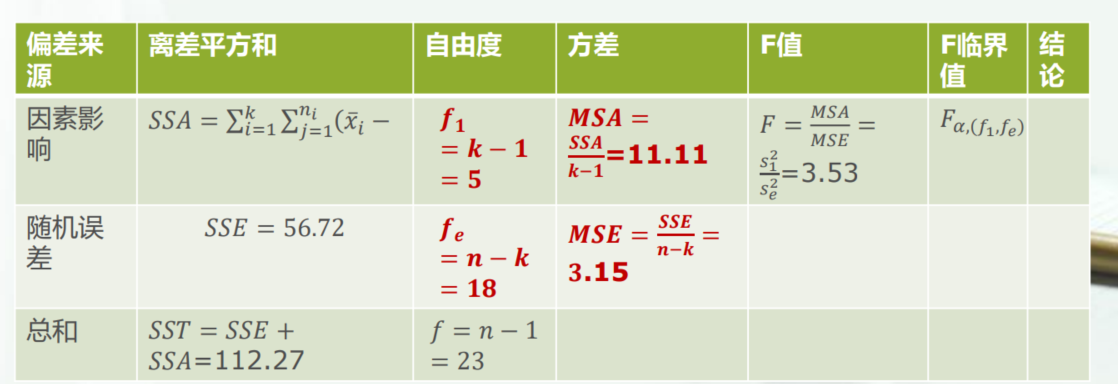
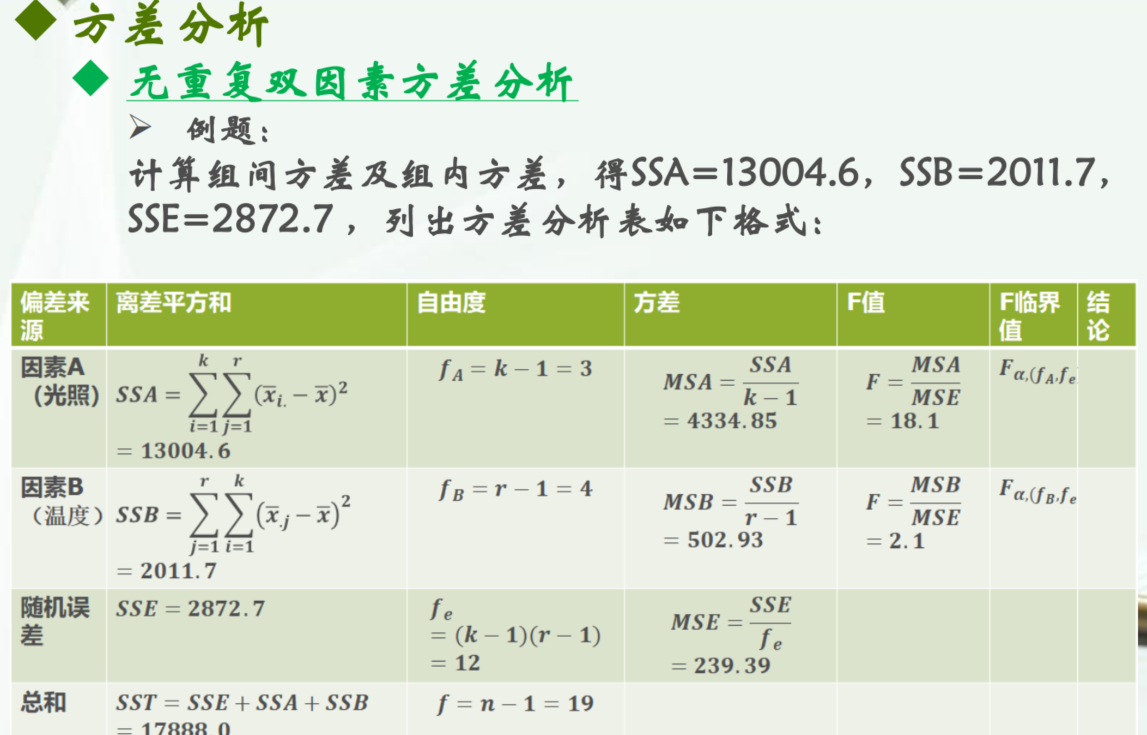
无重复双因素方差分析
其实一样的,就是每列如果也是有参数影响的话,每列再算一个MSB
例题:
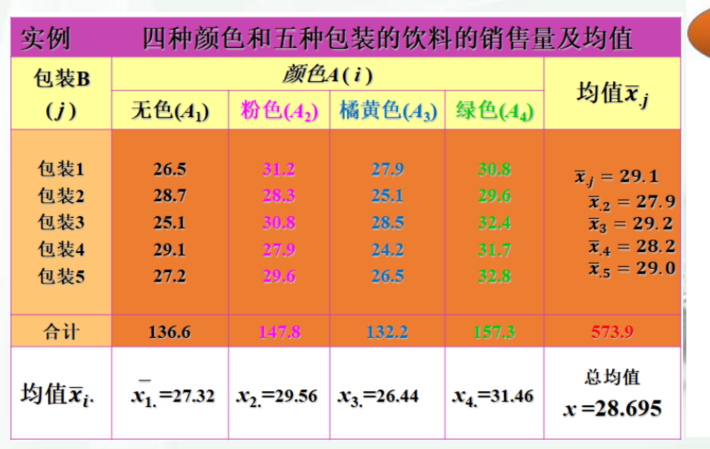
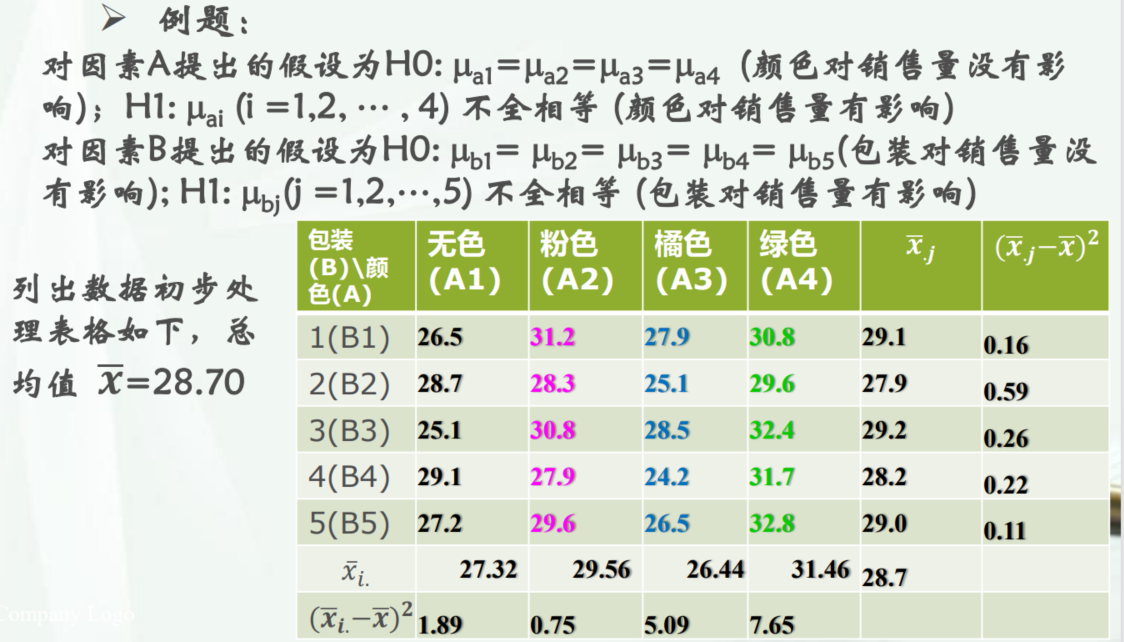
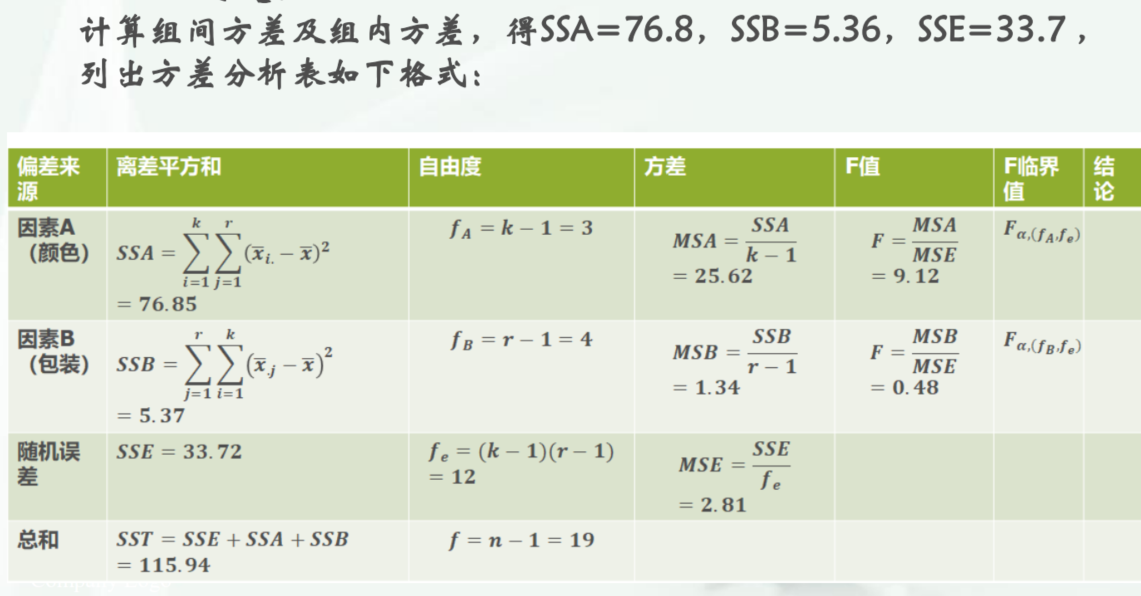

例题 2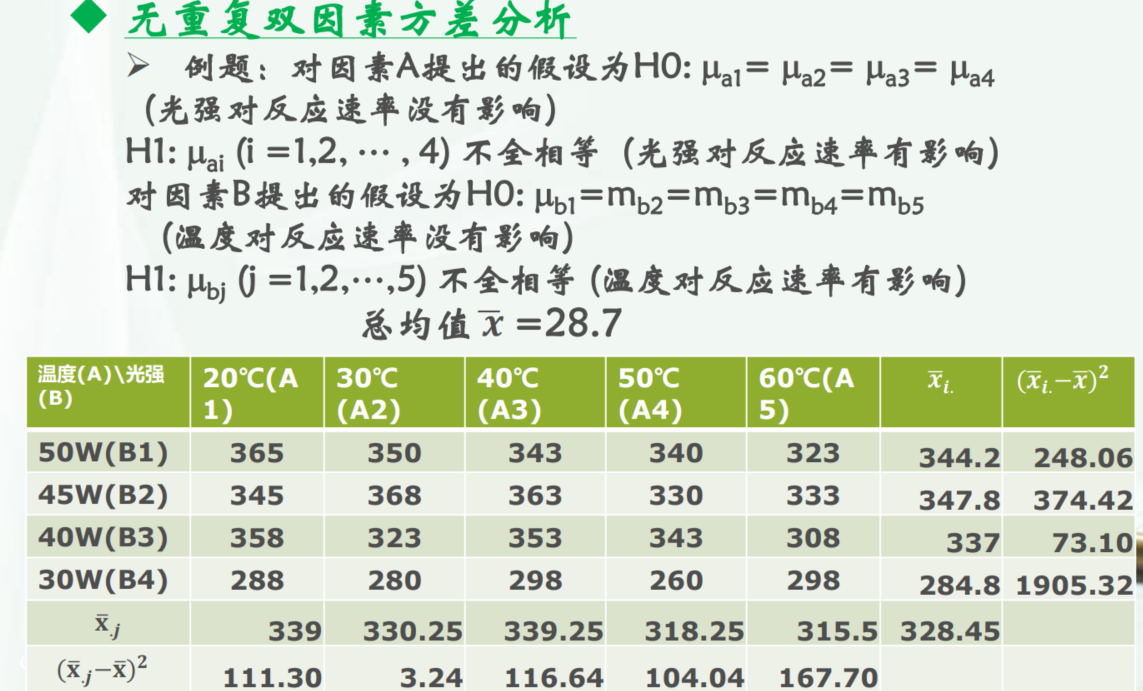

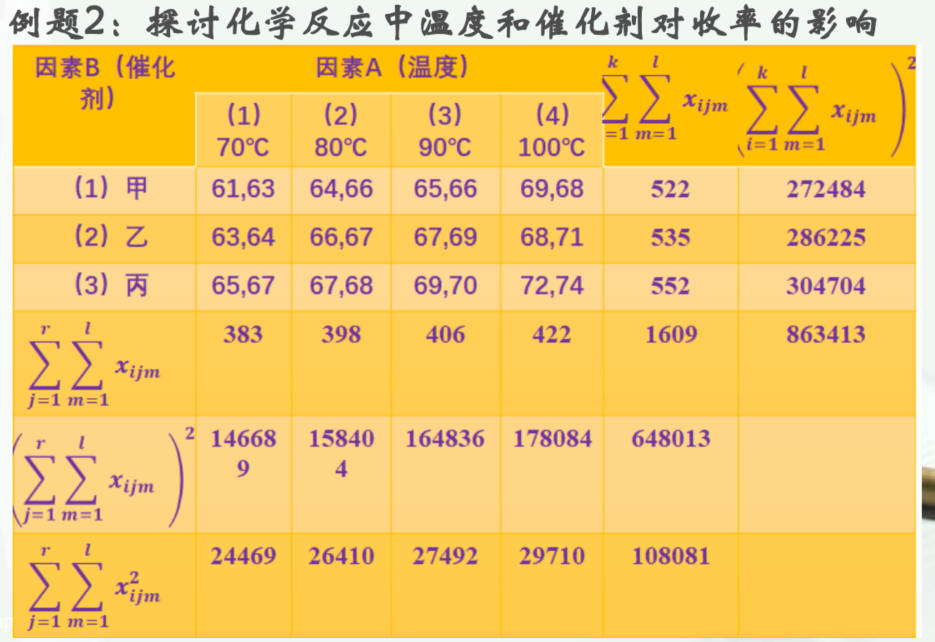
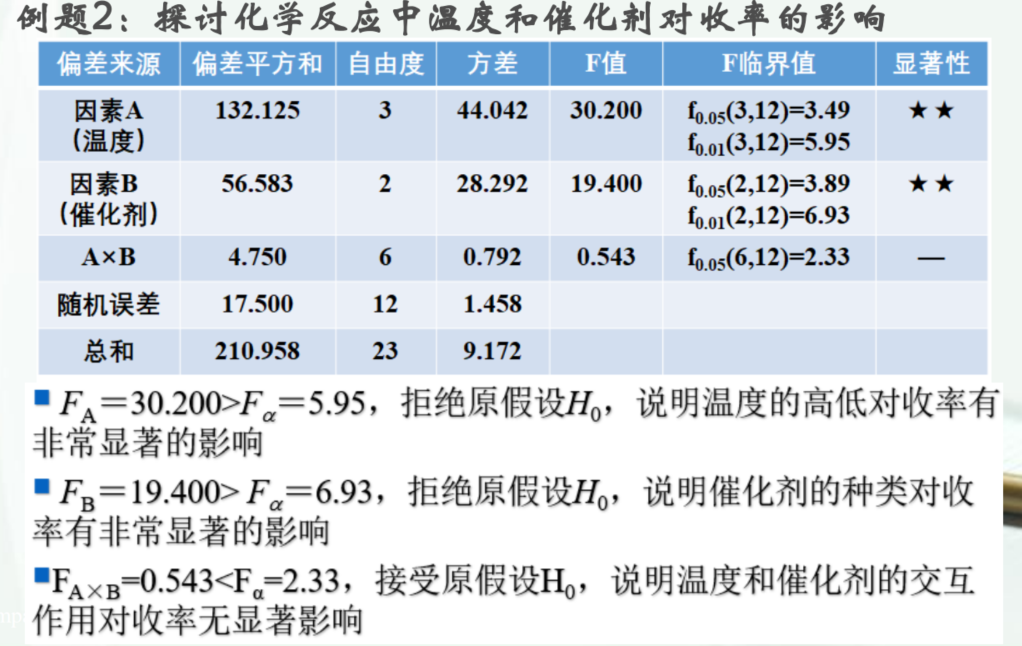
有重复双因素方差分析